INTRODUCTION

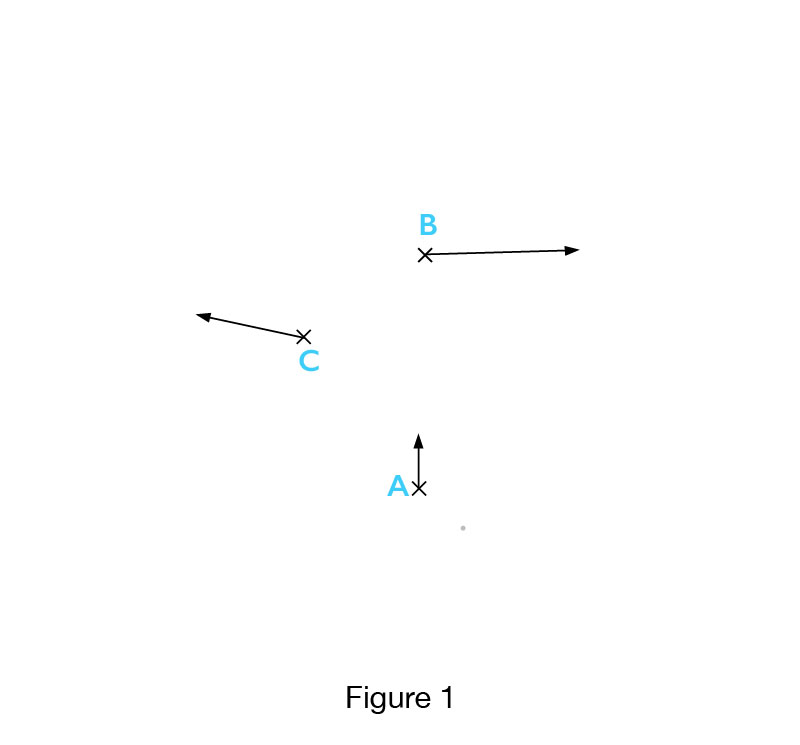
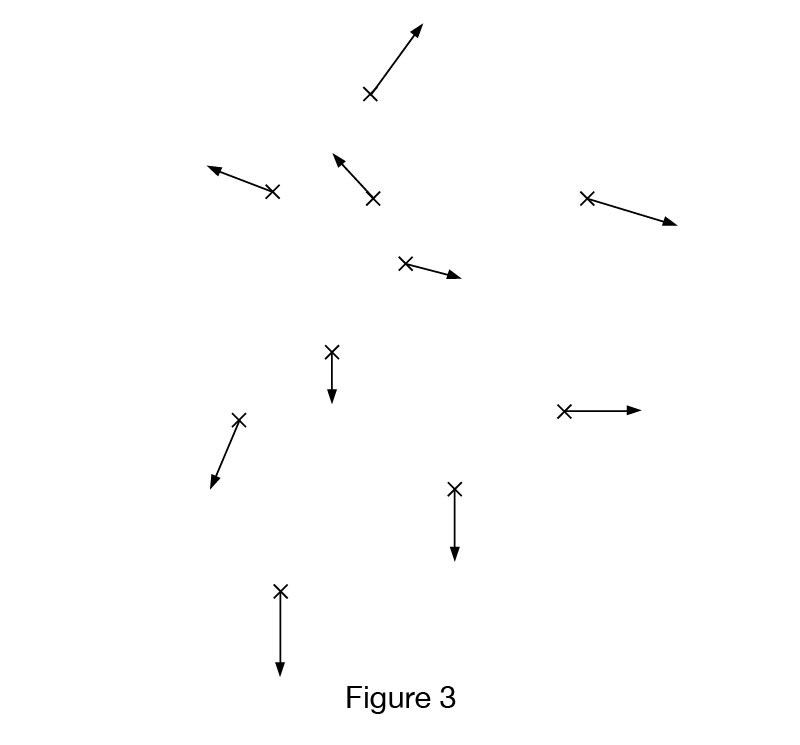
More distant the galaxies are, the faster they move away from us. This is an interesting phenomenon, there must be some reason for this movement of the galaxies. It is not likely that I will find the reasons why galaxies move a certain way (zero buget). However, let’s try to imagine the 3D Universe, or some of part of it, in 2D projection with imaginary galaxies marked with X and their velocity vectors Vx with associated directions and magnitudes. As far as imaginary galaxies are concerned in any part of the Universe, this seems to be quite simple, just assign each galaxy a vector V of a random direction and magnitude. When into this picture we try to incorporate the results of observing real galaxies, we find that velocity vectors have to fulfill certain conditions. Namely, observations have shown that all galaxies are moving away from us, and that the speed with which they are moving away from each other is proportional to their distance.

1. Limits and conditions for velocity vectors

This relationship of velocities and distances of real galaxies sets a number of conditions for vectors, the conditions that define the speed and direction of our imaginary 2D galaxies. First of all, it means that vectors of the same magnitude cannot be directed at the same point, and that they cannot be parallel if they are moving in the same direction. If they are moving in the opposite directions, then they cannot be aimed at one another. Likewise, vectors of different magnitudes can be parallel, and can be directed at the same point, but under the condition that the vector of smaller magnitude is always directed towards the vector of greater magnitude. The component of vector’s greater magnitude, parallel to the vector trajectory of lesser magnitude, must be is larger than smaller magnitude vectors (hereinafter: vectors larger and smaller). These are some of the major requirements for the directions and magnitudes of the velocity vectors (referred to as RfVV in the text below) of imaginary galaxies that prevent them from coming closer together, as this is contrary to astronomical observations of real galaxies. Next, we will only consider those RfVV velocity vectors that are in accordance with the specified limitations and conditions.

2. The rule of increasing distance

Limits and conditions for velocity vectors have produced the rule of increasing distance: Imaginary galaxies, in 2D projection, will be moving away from each other if their velocity vectors are in accordance with RfVV, i.e. with the abovementioned limitations and conditions on their directions and magnitude.

3. Imaginary galaxies

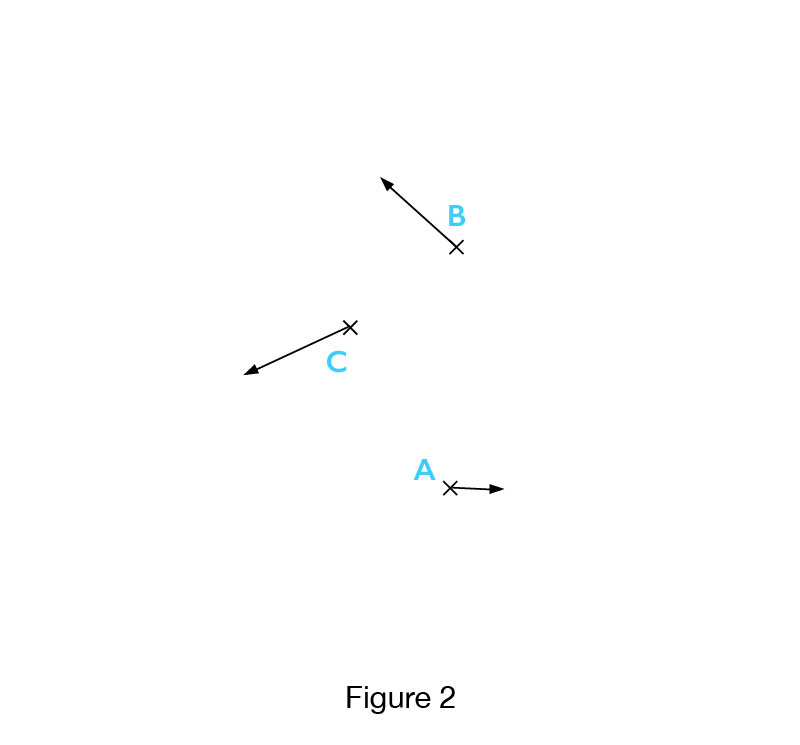
Using these constraints and conditions for velocity vectors ( RfVV), we can now construct our model (Fig.1) of imaginary galaxies in the 2D projection and their velocity vectors for a part of the imaginary Universe in accordance with the rules established by observations, which is the first step in the simulation of movement of real galaxies.

Figure 1 shows the galaxies A, B and C with their corresponding velocity vectors that are obviously in accordance with the provisions of galaxies that are moving away from each other, but it is also obvious that this is not a simple view of the possible movements of these galaxies, but that there is an infinite number of positions for vectors A, B and C all of which are in accordance with observational rules on the movement of galaxies, Fig.2.

This shows that the very rules on the velocity vectors’ directions and magnitudes are not sufficient to clearly define a general direction of motion for these imaginary galaxies, and that we need some additional rules for their positioning with respect to the directions and magnitude of their velocity vectors.

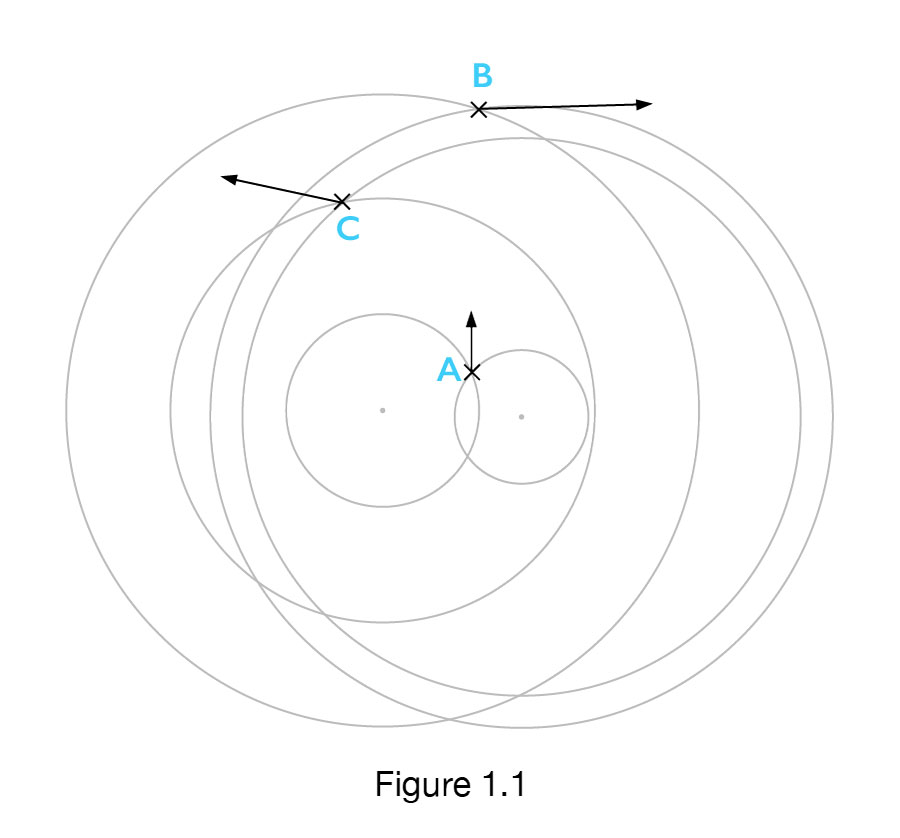
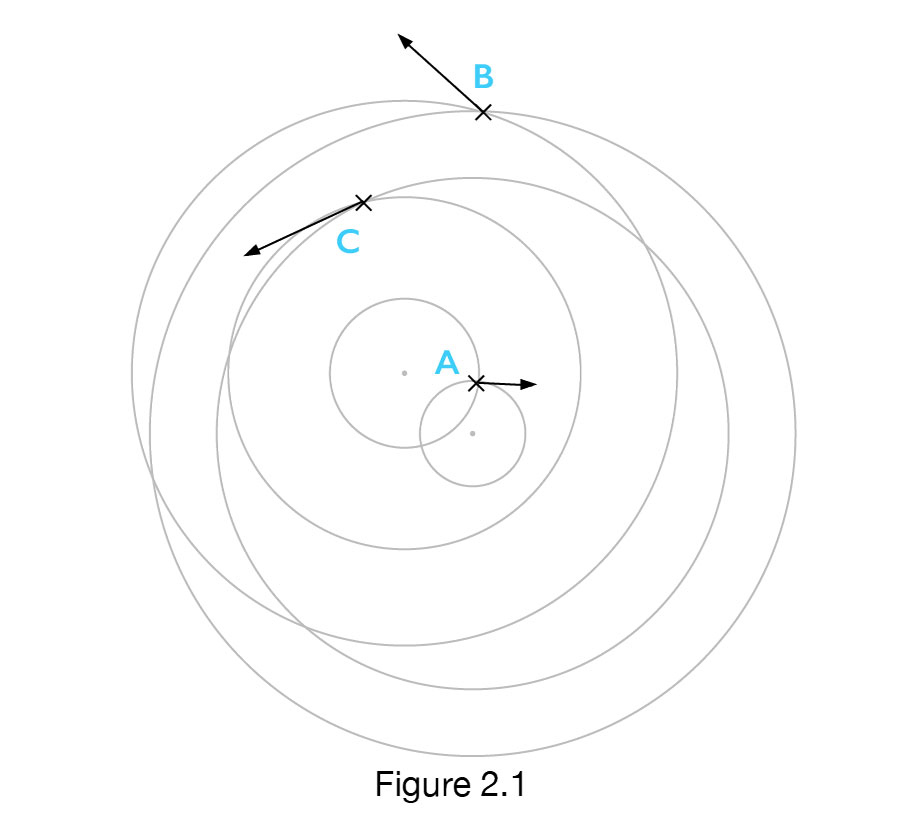
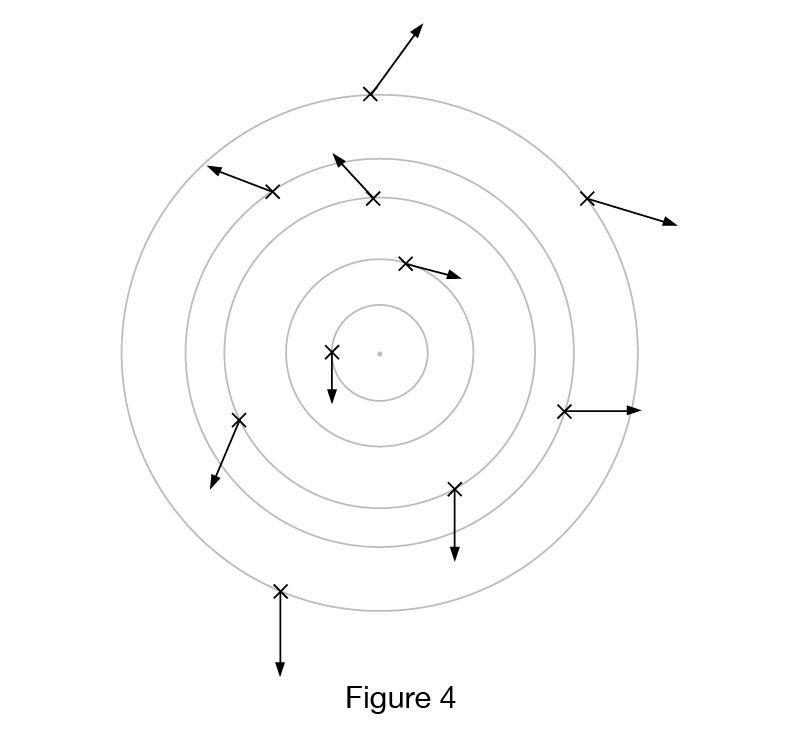
Observing the various configurations of the imaginary galaxies that fulfill the conditions of movement, I noticed that in all these cases, these imaginary galaxies can be placed on the concentric circles. By placing these concentric circles in Fig.1 and Fig. 2, we see these concentric circles in Fig. 1.1 and Fig. 2.1, with their center in So.

Since these concentric circuits can be placed on every (without exception) configuration of imaginary galaxies, whose velocity vectors fulfill the rules of galaxy movement from each other (RfVV), it is obvious that we have a new rule. The Rule of the Centre:

With every configuration of imaginary galaxies, velocity vectors fulfill the conditions of movement, where the galaxies are moving away from each other. The configuration has a center with conecentric cirlces around it and on these circles the imaginary galaxies are postioned.

The centre refers to the point around which these concentric cricles are postioned, the circles that contain imaginary galaxies.

In fact, from Figures 1.1, 2.1, we see that we do not have one point as the center of these circles, but we have a “centre space” in which the center is located. Therefore, any point in the ” centre space ” can be taken as a point of the center, so that the ” centre space ” will be referred to as the center. Due to the small number of galaxies in Figs 1 and 2, this center space is relatively large. As the number of imaginary galaxies increases, the center’s space is reduced.

This center, as well as spheres – circles, serve only to perform operations with velocity vectors.

The rule of movement where galaxies are moving away from each other, defines the configuration of the imaginary galaxies so that the ones with the slower speed are distributed closer to the center. Further away they are from the center, the speed of galaxies increases with the fact that at the same distance from the center, vectors always have the same magnitude and the general direction is opposite of the center. This means that in 2D projection, velocity vectors do not have to be radially positioned relative to the center, but that they can be at some angle, and with the general direction opposite to the center, Fig. 4.

This arrangement of imaginary galaxies follows from the above mentioned limitations and conditions for velocity vectors. Namely, lower-velocity vectors must be directed towards higher-velocity vectors, i.e. lower velocity vectors are “behind” them, and accordingly, at the same distance from the center, the vectors always have the same velocity.

The aforementioned rules for vectors set limits on their directions and magnitudes in relation to their position. This is especially noticeable with an increase in the number of imaginary galaxies in Figures 3 and 4, where the options for the directions and magnitude of the velocity vector are considerably reduced with respect to their position. Even this small number of imaginary galaxies in Fig. 3 shows some general direction of their movement. The position of the centre of the concentric circles (Figure 4) is important because it influences the validity of the picture on the general direction of movement of the galaxies, keeping in mind that the center at the same time also means the “center space”. Observations do not indicate the existence of a specific center or the general direction of the movement of real galaxies, but these observations do find that the galaxies move at certain speeds with magnitudes and directions, which means that their movement can be presented with velocity vectors in the 3D space. These vectors certainly fulfill the conditions of galaxy movement because de facto real galaxies are moving away from one another, which means that the Rule of the Center can be applied to the real galaxies: real galaxies are moving away from each other, and there is a Centre with the concentric spheres where real galaxies are located. So, it’s not a question of whether the Centre exists or not, the question is where is this Center of the Real Universe located?

The approach I used to position the centre of the imaginary gallaxes is not useful for real galaxies because for them we do not know the actual velocity vector, but we only know the components of the velocities by which the galaxies are moving away from us.

We now understand that for the development of a new model of the expansion of the Universe, the findings of the movement of galaxies arising from the observations are not sufficient, but that we require some additional information that we can find in the theoretical papers relating to the movement of galaxies and Universe expansion, and by looking at the existing models of expansion.

Although there are some models of the universe based on an analogy of everyday occurrences in our environment, they are lacking mathematical support that would prove the validity of the model in relation to the observations. This situation led me to develop a model of the movement of galaxies that is in line with the observations and basic theoretical findings in this field.

4. The basics of the Radical model of Universe expansion

The radical model is based exclusively on astronomical observations of the motion of the galaxies and their movement from each other. The only theoretical setting that this model uses is the creation of the Universe through Big Bang events.

4a. Theoretical basis of the model

The only theoretical setting we use in this model is (G. Lemaitre) of Big Bang theory that – an expanding Universe could be tracked back in time to an originating single point, point marked “So” in the pictures below. Based on this setting of G. Lemaitre, that Universe expansion started from a single point (So), this model sees post-Big Bang events as the expansion of space moving from the So center. Even though the observations have not confirmed the existence of this center, according to the Rule Center, we will further consider the Big Bang position as the center of the imaginary spheres on which the real galaxies are positioned.

4b. Observation basics of the model

As is well known, astronomer Edwin Hubble has observed galaxies and clusters and has found differences with their redshifts. This means that the Universe is not static, but that the galaxies move, and they are moving away from us at a rate that is proportional to their distance from us, regardless of the direction of observation. As it has long been established that the Milky Way is not in the center of the Universe, it means that the other galaxies are not only moving away from us, but moving away from each other and their velocity is proportional to their mutual distance. The expansion of the Universe and the increasing distance between the galaxies is a significant scientific discovery that did not, however, lead to the development of a valid model of the movement of galaxies that would be consistent with the observations. It’s not ruled out that there are valid models, but which for various reasons (e.g. no access to the relevant publications, marginalization …) did not get the attention they deserve. This brings us to an unusual situation. On one hand, with the excellent Big Bang theory we can explain the beginning of the Universe without us being there to witness it while on the other hand, we cannot explain with a valid model the events (movement of the galaxies) that are currently happening and which we observe in the present time.

5. Radical model

Observations show that galaxies are moving away from one another with speeds that are proportional to their distance, i.e., observations point to the velocities and their directions, and in this model the velocities and directions of the galaxy are defined by vectors of the corresponding magnitude and direction.

Based on G. Lemaitre’s statement that the expansion of the Universe begins from a singularity point (So), this model sees post-Big Bang events as an expansion of space moving from the center of So. According to this model, around this center, there are concentric spheres with the center in So. This is therefore the center of concentric circles from Figure 4, in 2D projection. Once again, the observations so far have not confirmed that there is a center as defined by the Big Bang theory. I use the Big Bang position as a virtual center to display vectors of the Galaxys movement.

These spheres are in the 2D projection shown in concentric circles in Figures 3 and 4.

The number of spheres is infinite but only those spheres are relevant which contain one or more galaxies on its surface. The spheres are not static, but they move as fast as galaxies on their surface. The galaxy positions in the 2D projection on the circles are marked with X. The direction of their motion is shown by the vectors that have V velocity.

Since the objective of the Radical model is to faithfully depict astronomical observations, the model allows velocity vectors with only those magnitudes and directions, and their positions, that will show the galaxies moving away from each other that’s proportional to their distance, while respecting the fundamentals of the Big Bang theory.

To meet the observational findings about the galaxies moving away from each other, the vectors’ magnitude on the same sphere have to be all equal and their directions are opposite of So (Big Bang).

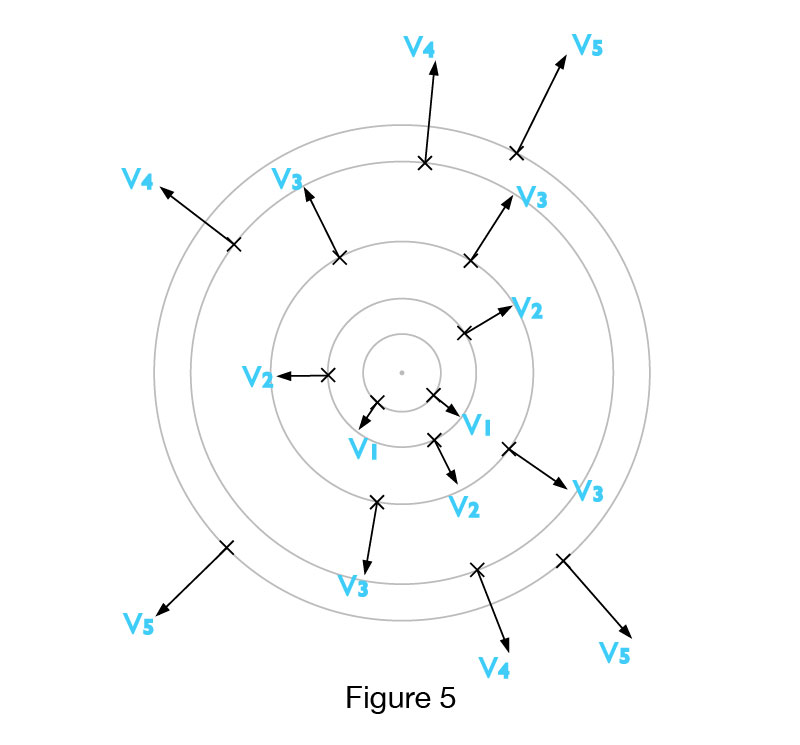
Aforementioned constraints to magnitude and direction of velocity vectors of galaxies, as well as incorporating Big Bang theory, are imagined in 2D projection, see Fig. 3. Galaxies with their positions and velocity vectors in this image are not depicted as real galaxies because they are no observational findings of the actual positions and speeds of each galaxy . Thus, the galaxies in Fig. 3 are imaginary with a random position, but with their velocity vectors pointing to them moving away from each other, which is proportional to the distance between them. We also see that with any positions of the galaxies on the same circle we always have results that are consistent with the observations. With Figures 4 and 5 it is apparent that in 2D projection we have two types of galaxies’ movement: Radial and Angled. Both will be further explained in detail. We will first consider the radial movement of the galaxy.

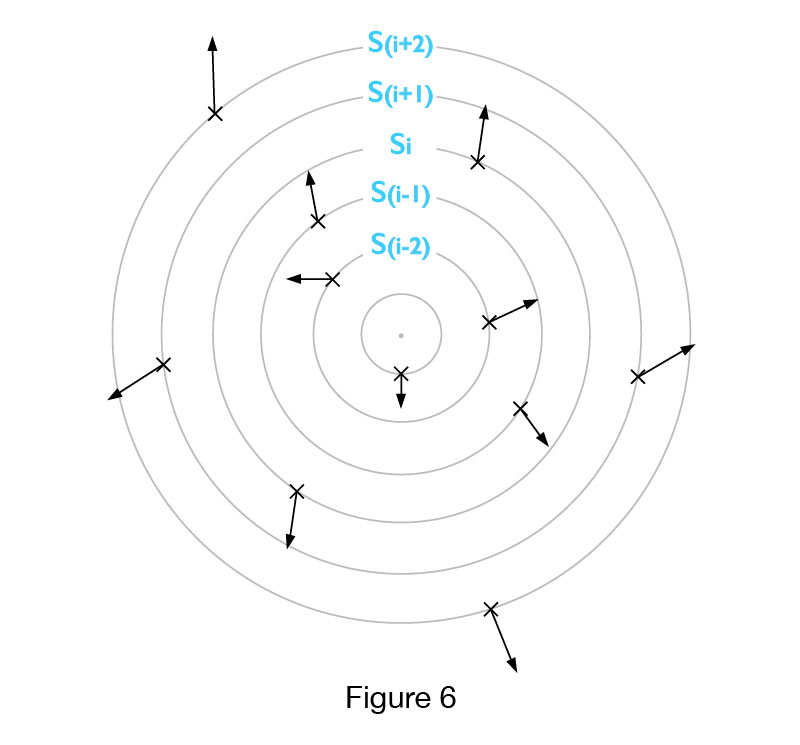
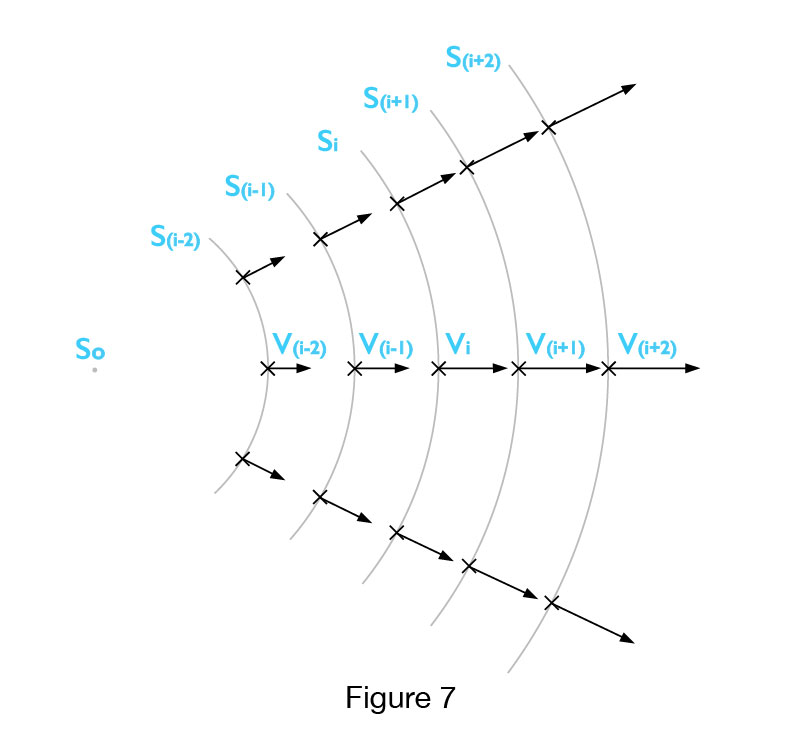
In order to confirm the validity of the Radical Model, we will simplify Fig. 5 so that galaxies at adjacent circles have a speed difference of one speed unit ‘su’ in some system of measurements (metric, imperial). Figure 6 also shows an arbitrary sphere Si and its neigbouring spheres projected in 2D.

We will first consider the radial movement of the galaxies. Fig.6 will be simplified so that velocity vectors are placed on the same radial lines as compared to So, Fig. 7.

Fig. 7 shows the part of the Universe in the 2D projection, which includes the circle Si and its adjacent circles S (i-2), S (i-1), S (i + 1) and S (i + 2). Galaxies that are on circle S (i-1) are 1 speed unit slower (1 su) than those on Si circle and the galaxies from S (I-2) circle are 2 speed units (2 su) slower than those on Si. Likewise, the galaxies on S (i + 1) circle are one speed unit 1 (1 su) faster than those that are located on Si circle while galaxies that are positioned on circle S (i + 2) move 2 speed (2 su) units faster compared to the ones on Si.

V(i-2)< V(I-1) <Vi <V (i + 1) <V (i + 2)
Vi – V(i-1) = 1 su , V(i-1) = Vi – 1su V (i + 2) -V (i-2) = 4 su, V (i + 2) = V(i-2) + 4 su
Vi – V(i-2) = 2 su , V(i-2) = Vi – 2 su , V(i+2) – Vi = 2 su , V(i+2) = Vi + 2 su

Where “su” is determined with

Su = lu / T lu = su x T

Hence, the length unit (lu) is equal to the speed unit multiplied by the unit of time. In a unit of time T, the galaxy from the sphere Si will travel the path I(i) = V (i) x T,

the galaxy from S(i+1) will travel the path l(i+1)= V(i+1) xT , the galaxy from S(i+2) will travel the path l(i+2) = V(i+2) x T , the galaxy from S(i-1) will travel the path l(i-1) = V(i-1) xT , the galaxy from S(i-2) will travel the path l(i-2) = V(i-2) xT

As lu = su x T      we get l (i-2) = l (i) -2lu
l (i-1) = l (i) -1 lu
l (i + 1) = l (i) + 1lu
l (i + 2) = l (i) + 2lu

Likewise, in the unit of time T we will get:

l (i-5) = l (i) – 5 lu , l (i + 5) = l (i) + 5 lu

So after time T, the distance between the galaxies on circles S (i-5) and Si will increase by 5 length units, and the distance between the galaxies on circles S (i-5) and S (i + 5) galaxies will increase by 10 length units.

For galaxy speeds we have: V (i-5) = V (i) – 5 su, V (i + 5) = V (i) + 5su

We see that galaxies from the S(i) circle have speed that is 5 speed units greater than the galaxies on circle S (i-5) while the galaxies located on S (i + 5) circle have a speed of that’s 10 speed units faster from the galaxies on S ( I-5) circle.

That is exactly what has been confirmed in the observations: all galaxies are moving away from us, and their speed is proportional to their distance. As I mentioned earlier, the Milky Way is not in the center of the Universe, which means that observations from any other galaxy would yield the same results, i.e. the galaxies are moving away from each other and their speed is proportional to their distance.

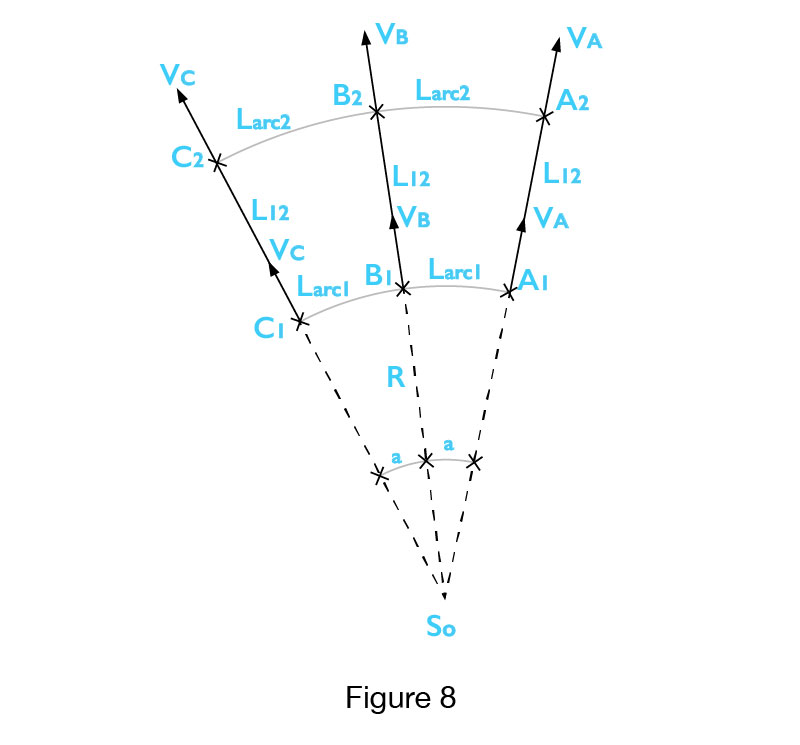
Besides the radial, we also have the angled movement of galaxies. Here, it will be presented within the Radical model where all galaxies that are located on the same sphere, i.e. at the same distance from So (Big Bang), have the same magnitude of the velocity vector, and that these vectors are at a certain angle. The angle labeled “a” is shown in the 2D projection in Figure 8. There you can see the imaginary galaxies A, B and C at the distance R of So (Big Bang). The arc distance between A1 and B1 positions of galaxies A and B is indicated by Larc1.

Larc1 = ax R, where “a” is the angle A1-So-B1, expressed by radians.

In the unit of time T, galaxies A and B will come from positions A1 and B1 into positions A2 and B2, i.e. they will go to

L12 = V xT           where: VA = VB = VC = V

In the new positions A2 and B2 we have Larc2, the arc distance between A2 and B2

Larc2 = a x (R + L12)

Larc2 – Larc1 = a x R + a x L12 – a x R = a x L12

The velocity vector of the galaxy C is at an angle “a” in relation to the velocity vector of the galaxy B while the magnitudes of the velocity vectors of the galaxies VB and VC are equal because they are on the same circle, i.e. at the same distance from So (Big Bang). Thus, the length L12 between the positions C1 and C2 will be identical to the lengths L12 between A1 and A2 as well as B1 and B2. For the distance between galaxies A and C we have:

L (arcA1C1) = 2 a x R                L (arcA2C2) = 2 a x (R + L12)

Thus, in the unit of time T, the galaxy A has moved away from galaxy B by: a x L12, and at the same time from galaxy C by:

L (arcA2C2) – L (arcA1C1) = 2a x (R + L12) – 2a x R = 2a x L12

[L (arcA2C2) – L (arcA1C1)] / [Larc2-Larc1] = 2a x L12 / ax l12 = 2

We see that in the unit of time T, the distance between the galaxies A and C has increased twice as much as the distance between the galaxies A and B. Since, by definition, the velocity is determined by the spanned distance in the unit of time, we can now define the velocities of the galaxies A, B and C that are moving away from each other (Vab, Vac . We will thus divide the lengths of galaxy separations (as they are moving away from each other) with the unit of time T during which the galaxy movement has occurred. Thus, the velocity by which the galaxies A and B are moving away from each other (Vab) is equal to:

Vab = (a x L12) / T, and the velocity by which the galaxies A and C are separating is: Vac = (2a x L12) / T

Relationship between Vac and Vab is:

Vac / Vab = [(2 a xl 12) / T] / [(a x l12) / T] = 2

Thus, the increasing distance of galaxy C from galaxy A is twice as fast as the one of galaxy B from galaxy A.

According to observations: the farther galaxies are, the faster they move away from us, which is faithfully depicted by the Radical model in the 2D projection. Its full validity is maintained by the Radical Model in 3D projection as it is only about transitioning from 2D vector to 3D vectors without changing Radical model settings.

Radical model of universe expansion

The Radical Model of the universe expansion sees the universe with a center in the Big Bang position, from which the galaxies are radially moving away. The speeds of the galaxies are increasing faster as they are further away from the cnter. All galaxies that are located at the same distance from the center have the same speed.

Remarks

* I have presented a strong argument of the Radical Model and we have to ask ourselves if there are any weaknesses in it? As observations and the Big Bang theory are the foundation of this model, its weak points should be sought in these two places. The Big Bang theory is generally accepted, though there are some alternatives. One of them is the oscillating universe, which intermittently expands and contracts. In regards to the Radical Model, it does not matter whether this is the first or tenth expansion of the universe, and this alternative to Big Bang theory is irrelevant.

The idea of ​​multiverse is not yet clearly defined and there are no observational findings to support it thus this theory is not taken into consideration during the development of the Radical Model.

The Radical model is entirely in line with what the observations have established: that galaxies are moving away from each other at a rate that is proportional to the distance between them. The radical model does not make any claims that were not validated by observation, such as that the movements of the galaxies do not seem to have a special point as a ” center “. So here I had the choice: Consider the generally accepted Big Bang theory which claims that there is a center, or consider what the observations so far have not found, but possibly exists. The Big Bang Theory is backed up by some valid proofs, while observations have not shown the existence of one or more centers suggesting a decentralization model of the universe, according to which, in the end, each galaxy is a kind of a center. It is obvious that from this comes that the decentralized model, that is derived from observations, contradicts the Big Bang theory.

* In addition to the presented evidence of validity of the Radical Model, this model could for some reason be rejected or marginalized. Given the strong link of this model with observational findings and Big Bang theory, this would also mean rejecting or marginalizing observation findings and Big Bang theory.

* In Figure 4, with imaginary galaxies set at different distances, we show the simplest but not the only way to prove the validity of the Radical Model. Validating this model with galaxies in random positions (Fig. 3) would take much more space and time for the same final result. In any case, however we position the imaginary galaxies, we have to keep the basic settings of the Radical Model, because only this model fully mathematically satisfies the observational findings.

* In order to determine the movement of some random galaxies that are not on the same radius line or in the same sphere, we can employ a separate consideration of radial and angular movement of galaxies and then unify the results.

Conclusion

The Radical Model is the only model of the expansion of the universe that directly connects observational findings of galaxies movement away from each other with the Big Bang theory. This linking of observations with the theory has led to the conclusion that the galaxy velocities are lower closer they are to the Big Bang position, suggesting the increase of the galaxies’ mass near the centre.